Elipse

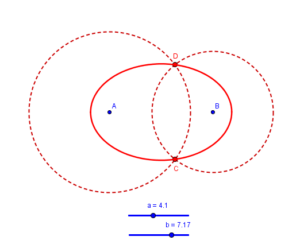
Las cónicas aparecen como lugares geométricos definidos por propiedades de puntos en el plano. Así la elipse puede definirse como el lugar geométrico de los puntos del plano cuya suma de distancias a otros dos puntos fijos llamados focos, es constante. La realización práctica pasa por tomar dos circunferencias cuyos radios son de suma constante, por ejemplo a y b-a: los puntos en la intersección de ambas, C y D, estarán a distancia fija b de los centros de las mismas, A y B, que serán los focos de la elipse. Variando a se obtiene una elipse dada, y variando b distinto semieje mayor de esta.

Parábola

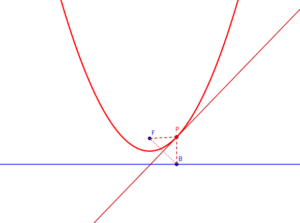
La parábola se define como el lugar geométrico de los puntos del plano cuya distancia a un punto fijo llamado foco es igual a la distancia a una recta fija llamada directriz. La realización práctica se obtiene tomando triángulos isósceles BFP, con uno de los vértices, B, apoyados en la recta directriz y otro sobre el punto fijo F. Al ser isósceles los otros dos lados serán de igual valor, lo que da la condición de que el punto P este a igual distancia del foco fijo F que de la recta directriz.

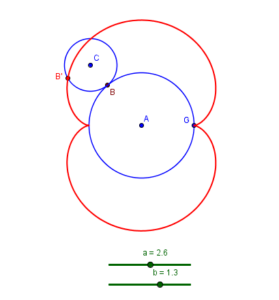
Otros muchos lugares geométricos aparecen cuando consideramos propiedades relacionadas con el movimiento de un objeto respecto a otro. Así la epicicloide se define como el lugar geométrico dado por un punto sobre una circunferencia de centro C, que va recorriendo el exterior de otra de centro A, de forma que ambas se mantienen tangentes por un punto cambiante, B. Para conseguir dibujarla hacemos que el punto B´ vaya moviéndose según el ángulo con el que se mueve el punto B con respecto a un punto fijo D, según un movimiento de rotación. Pero para conseguir que el efecto de movimiento sea real, debemos incrementar esa rotación con la proporción a/b, siendo a y b los radios de la circunferencia interior y exterior, y que nos dan, a su vez, la relación entre el perímetro de una y otra.

Epicicloide

En el ejemplo representado (imagen de la izquierda) el radio de la circunferencia exterior (pequeña) es la mitad del de la circunferencia interior (grande), con lo que al rodar una sobre otra la pequeña da dos vueltas mientras recorre una vuelta de la grande al ser su perímetro la mitad. El lugar geométrico recorrido por un punto fijo moviéndose es el señalado en color rojo y da lugar a un caso particular de epicicloide que se denomina nefroide, por su parecido con un riñón.

Los lugares geométricos nos permiten resolver una multitud de problemas en campos tan diversos como la física, la arquitectura, la cartografía, la ingeniería, en particular la ingeniería mecánica y de control o hasta la química. Sin duda una herramienta matemática versátil.

Referencias del artículo:

1. Geography and political power: The Geography of nations and states. Peter M. Slowe. Routledge Library Editions.

2. Geometría Analítica. Charles H. Lehmann. Editorial Limusa. 2012.